VECTORS
Displacement and Positions of Vectors
The Concept of a Vector Quantity
Explain the concept of a vector quantity
A vector - is a physical quantity which has both magnitude and direction.
The Difference Between Displacement and Position Vectors
Distinguish between displacement and position vectors
If an object moves from point A to another point say B, there is a displacement
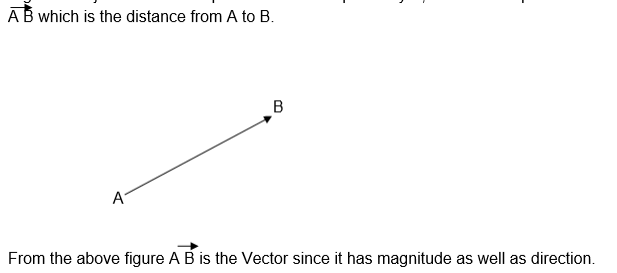
There are many Vector quantities, some of which are: displacement, velocity, acceleration, force, momentum, electric field and magnetic field.
Other physical quantities have only magnitude, these quantities are called Scalars.
For example distance, speed, pressure, time and temperature
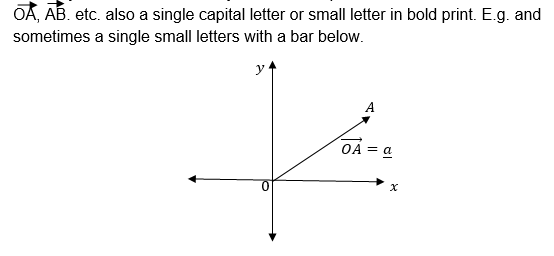
Naming of Vectors:
Normally vectors are named by either two capital letters with an arrow above e.g.

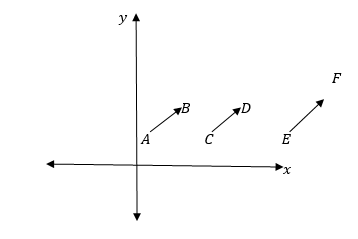
Equivalent Vectors:

Therefore two or more vectors are said to be equivalent if and only if they have same magnitude and direction.
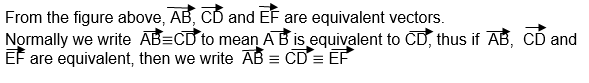
Position Vectors;
In the x —plane all vectors with initial points at the origin and their end points elsewhere are called position vectors. Position vectors are named by the coordinates of their end points.
Consider the following diagram.
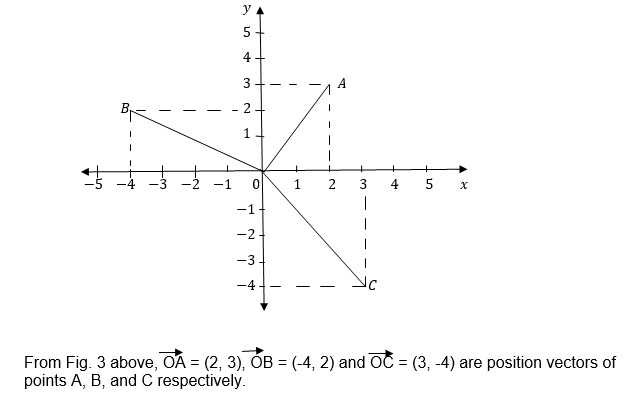
Components of position vectors:

Example 1
Write the position vectors of the following points: (a) A (1,-1), (b) B (-4,-3)
(c) C= (u, v) where U and V are any real numbers and give their horizontal and vertically components

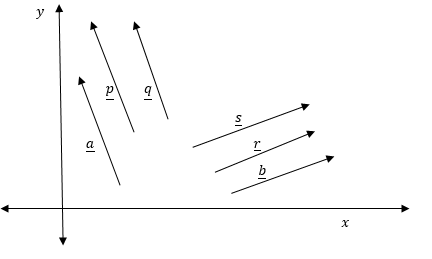
Example 2
For each of vectors a and b shown in figure below draw a pair of equivalent vectors

Solution:
The following figure shows the vectors a and b and their respective pairs of equivalent vectors
Any Vector into I and J Components
Resolving any vector into I and J components
The unit Vectors i and j.
Definition: A unit vector is a position vector of unit length in the positive direction of x axis or y axis in the xy—plane.
The letters iand jare used to represent unit vectors in the X axis and y – axis respectively.
Consider the following sketch,


Example 3
Write the following vectors in terms of i and j vectors:
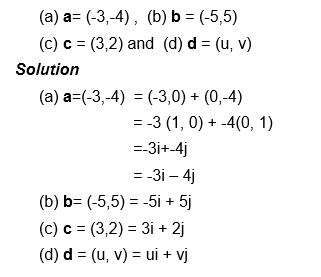
Example 4
Write the following vectors as position vectors.

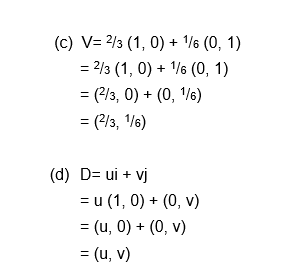
Magnitude and Direction of a Vector
The Magnitude and Direction of a Vector
Calculate the magnitude and direction of a vector
Magnitude (Modules) of a Vector
Definition: The magnitude / modules of a vector is the size of a vector, it is a scalar quantity that expresses the size of a vector regardless of its direction.
Finding the magnitude of given vector.
Normally the magnitude of a given vector is calculated by using the distance formula which is based on Pythagoras theorem.
Using Pythagoras theorem

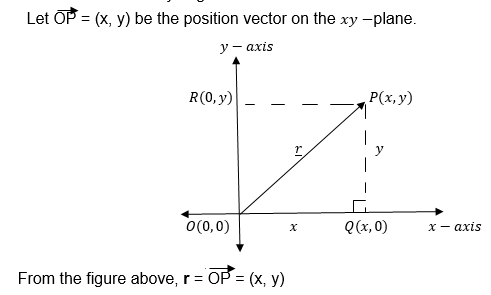
Example 5
Calculate the magnitude of the position vector v=(- 3 , 4)
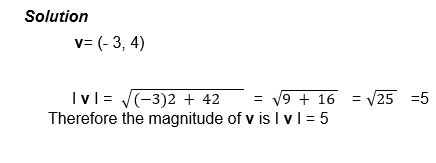
What is the magnitude of the vector U if U = 4i – 5j?
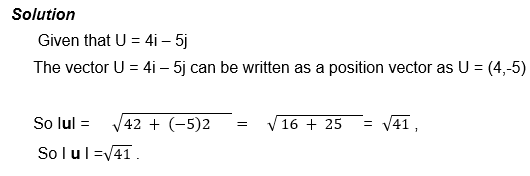
Unit Vectors:
Definition: A unit of Vector is any vector whose magnitude or modulus is one Unit.
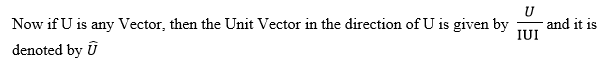
Example 6
Find a Unit Vector in the direction of Vector U = (12, 5)

Direction of a vector:
The direction of a Vector may be given by using either bearings or direction Cosines.
(a) By Bearings:
Bearings are angles from a fixed direction in order to locate the interested places on the earth's surface.
Reading bearings: There are two method used to read bearings, in the first method all angles are measured with reference from the North direction only where by the North is taken as 0000, the east 0900, the South is 1800 and West 2700
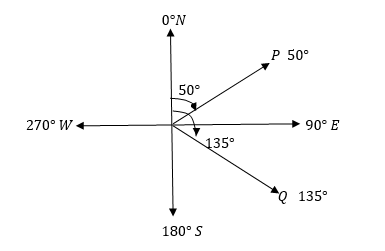
From the figure above, point P is located at a bearing of 0500, while Q is located at a bearing of 1350.
Commonly the bearing of point B from point A is measured from the north direction at point A to the line joining AB and that of A from B is measured from the North direction at point B to the line joining BA.
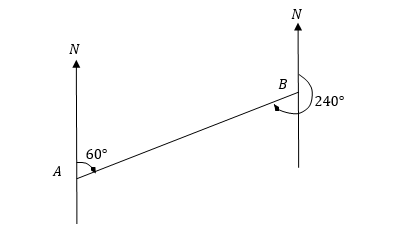
From the figure above the bearing of B from A, is 0600 while that of A from B is 2400 In the second method two directions are used as reference directions, these are North and south.
In this method the location of places is found by reading an acute angle from the north eastwards or westwards and from the south eastwards or westwards.
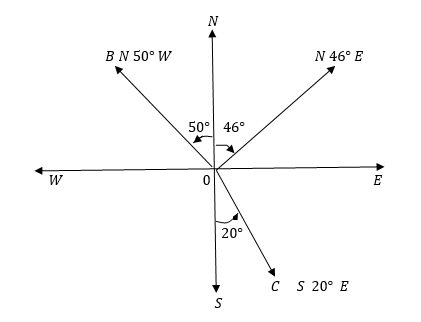
From figure above, the direction of point A from O is N 460 E , that of B is N500W while the direction from of C is S200E.
Example 7
Mikumi is 140km at a bearing of 0700f from Iringa. Makambako is 160km at bearing of 2150 from Iringa. Sketch the position of these towns relative to each other, hence calculate the magnitude and direction of the displacement from Makambako to Mikumi.

Sketch
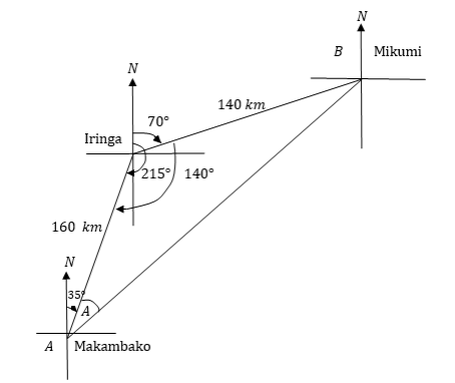
Using the cosine rule

The displacement from Makambakoto Mikumiis 12 286kmBy sine rule
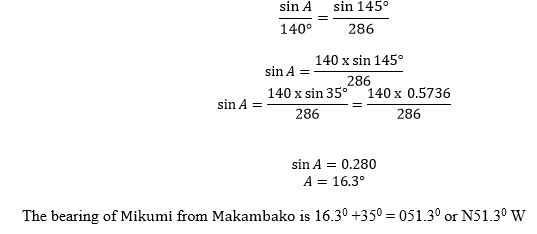
Alternatively by using the scale AB is approximately 14.3 cm Therefore AB = 14.3x 20 km = 286km and the bearing is obtained a protractor which is about N510E
(b) Direction cosines
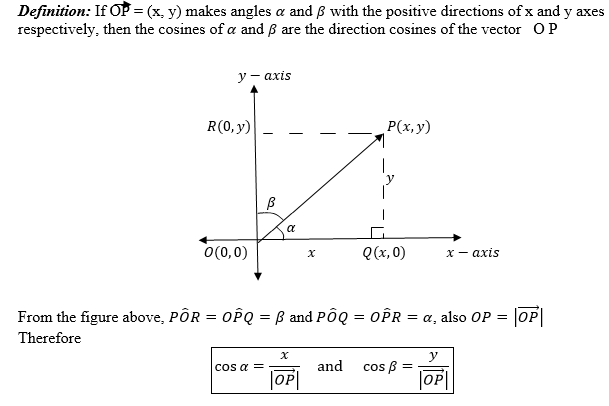
Where Cos A and Cos B are the direction cosines of OP
Example 8
If a = 6i + 8j find the direction cosine of a and hence find the angle made by a with the positive x – axis.
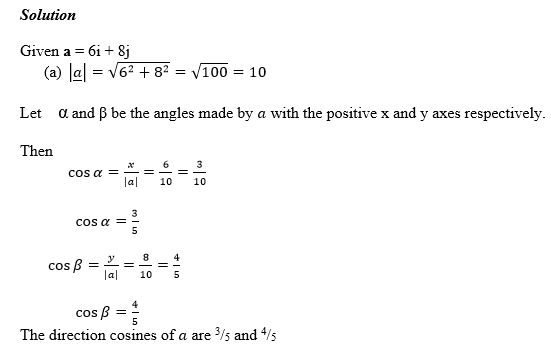
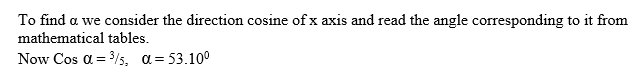
Exercise 1
1. Find the magnitude of

Sum and Difference of Vectors
The Sum of Two or More Vectors
Find the sum of two or more vectors
Addition of vectors
The sum of any two or more vectors is called the resultant of the given vectors. The sum of vectors is governed by triangle, parallelogram and polygon laws of vector addition.
(1) Triangle law of vector Addition
Adding two vectors involves joining two vectors such that the initial point of the second vector is the end point of first vector and the resultant is obtained by completing the triangle with the vector whose initial point is the initial point of the first vector and whose end points the end point of the second vector.
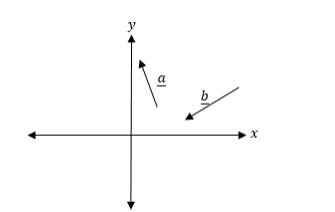
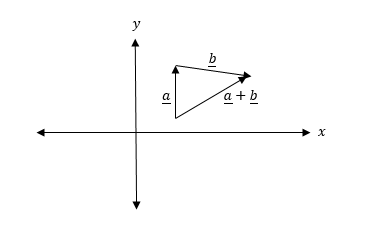
From the figure above a + b is the resultant of vectors a and b as shown below
(2) The parallelogram law
When two vectors have a common initial point say P, then their resultant is obtained by completing a parallelogram, where the two vectors are the sides of the diagonal through P and with initial point at P
Example 9
Find the resultant of vectorsuandvin the following figure.
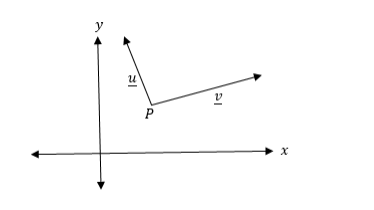
Solution
To get the resultant of vectors u and v, you need to complete the parallelogram as shown in the following figure
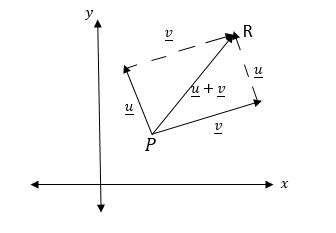
From the figure above, the result of u and v is PR = U + V = U + V
Note that by parallelogram law of vector addition, commutative property is verified.
Polygon law of vector addition:
If you want to add more than two vectors, you join the end point to the initial point of the vectors one after another and the resultant is the vector joining the initial point of the first vector to the end point of the last vector
Example 10
Find the resultant of vectors a, b, c and d as shown in the figure below.
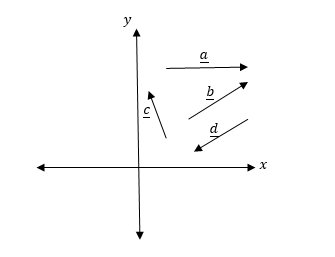
Solution
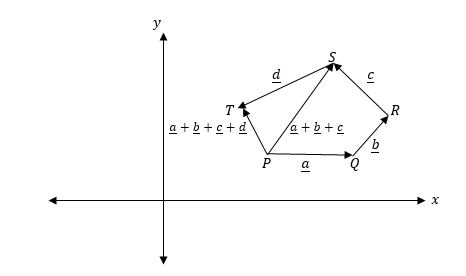
In the figure above P is the initial point of a, b has been joined toaat point Q and c is joined to b at R, while d is joined to c at point S and PT = a + b + c + d which is the resultant of the four vectors.
Opposite vectors
Two vectors are said to be opposite to each other if they have the same magnitude but different directions
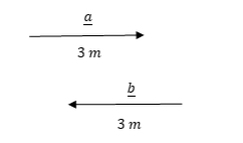
From the figure above a and b have the same magnitude (3m) but opposite direction.
So a and b are opposite vectors.
Opposite vectors have zero resultant that is if a and b are opposite vectors, then
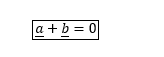
Example 11
Find the vector p opposite to the vector r = 6i – 2j

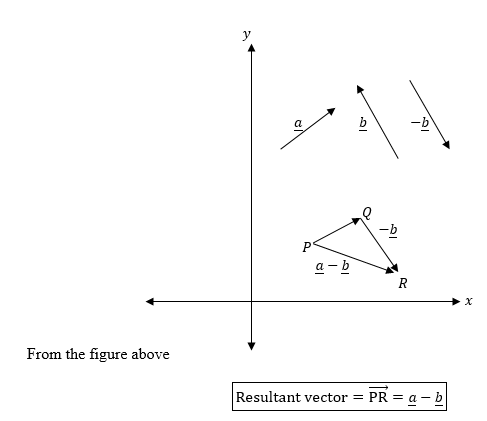
The Difference of Vectors
Find the difference of vectors
Normally when subtracting one vector from another the result obtained is the same as that of addition but to the opposite of the other vector.
Therefore the different of two vector is also the resultant vector
Consider the following figure
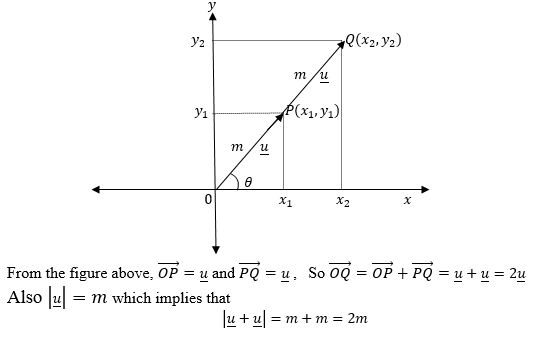
Multiplication of a Vector by a Scalar
A Vector by a Scalar
Multiply a vector by a scalar
If a vector U has a magnitude m units and makes an angleθwith a positive x axis, then doubling the magnitude of U gives a vector with magnitude 2m.
Generally if U = (u1, u2) and t is any non zero real number while (u1, u2) are also real numbers, then
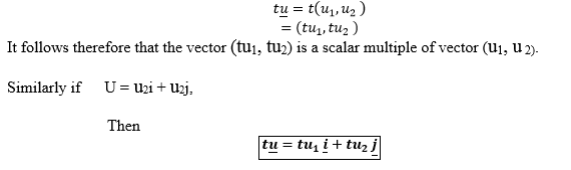
Example 12
If a = 3i + 3j and b = 5i + 4j
Find – 5a + 3b
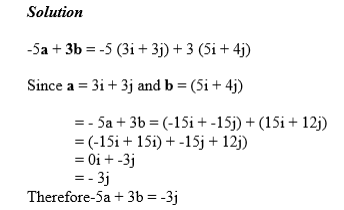
Example 13
Given that p = (8, 6) and q = (7, 9). Find 9p – 8q
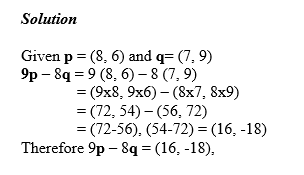
Application of Vectors
Vectors in Solving Simple Problems on Velocities, Displacements and Forces
Apply vectors in solving simple problems on velocities, displacements and forces
Vector knowledge is applicable in solving many practical problems as in the following examples.
A student walks 40 m in the direction S 450 E from the dormitory to the parade ground and then he walks 100m due east to his classroom. Find his displacement from dormitory to the classroom.
Solution
Consider the following figure describing the displacement which joins the dormitory D. parade ground P and Classroom C.
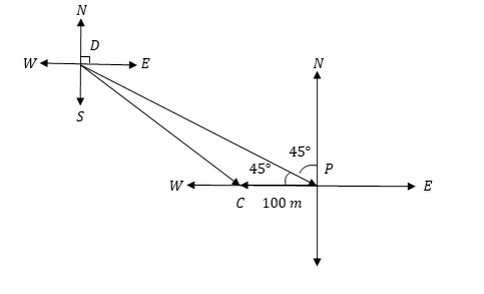
From the figure above the resultant is DC. By cosine rule

Example 14
Three forces F1 = (3,4), F2 = (5,-2) and F3 = (4,3) measured in Newtons act at point O (0,0)
- Determine the magnitude and direction of their resultant.
- Calculate the magnitude and direction of the opposite of the resultant force.
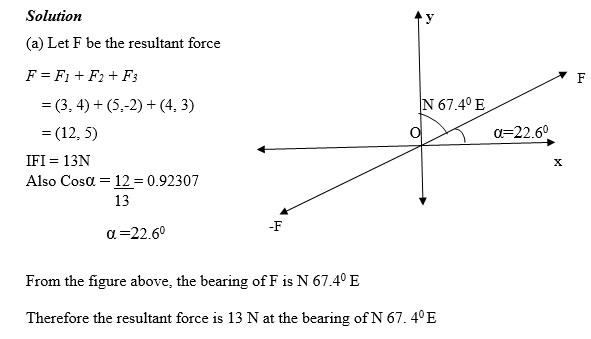
(b) Let the force opposite to F be Fo, then Fo = -F = - (12, 5) = (-12, -5)
Fo= 13N and its bearing is (67.40+1800) = 247.40
So the magnitude and direction of the force opposite to the resultant force is 13N and S67.40W respectively..
Exercise 2
1. Given that U = (3, -4), V= (-4, 3) and W = (1, 1), calculate.
- The resultant of U + V + W
- The magnitude and direction of the resultant calculated in part (a) above.
2. A boat moves with a velocity of 10km/h upstream against a downstream current of 10km/h. Calculate the velocity of the boat when moving down steam.
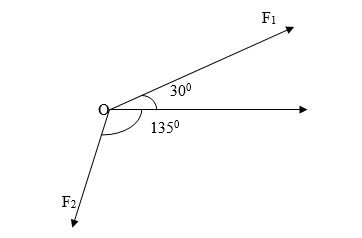
3. Two forces acting at a point O makes angles of 300 and 1350 with their resultant having magnitude 20N as shown in the diagram below.
4. Calculate the magnitude and direction of the resultant of the velocities V1=5i + 9j,V2 = 4i + 6j and V3 = 4i – 3j where i and j are unit vectors of magnitude 1m/s in the positive directions of the x and y axis respectively.