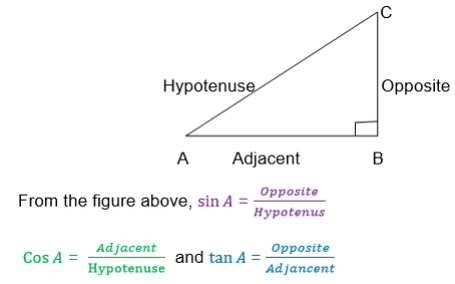
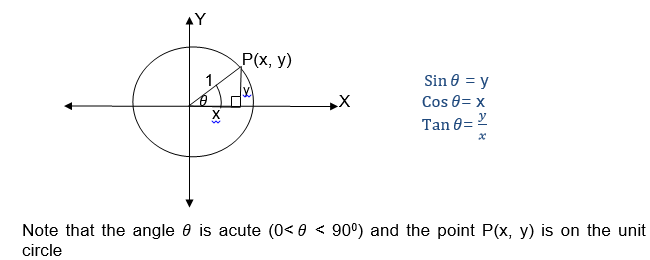
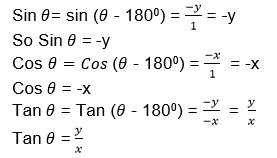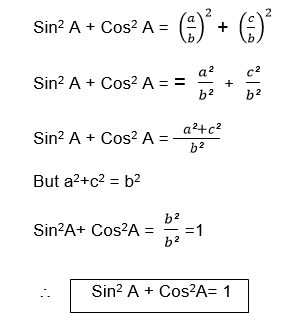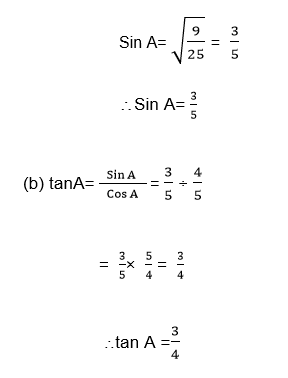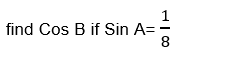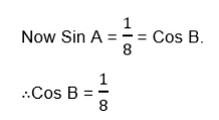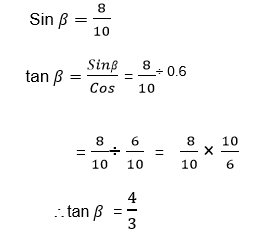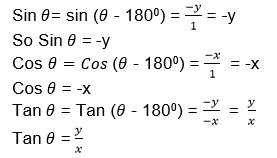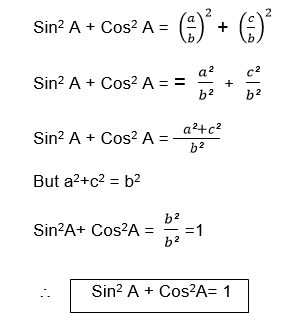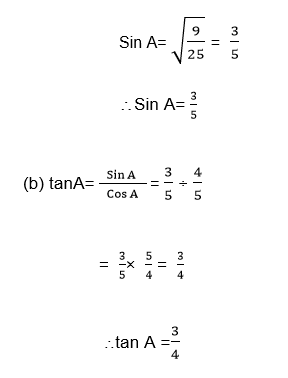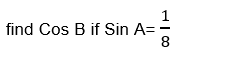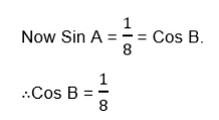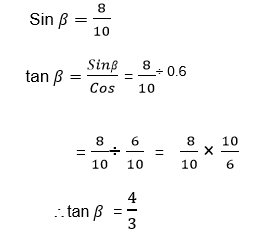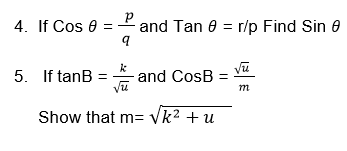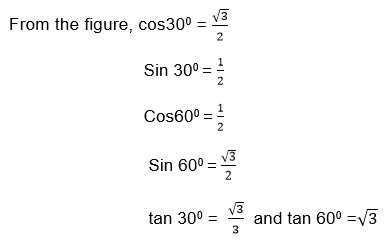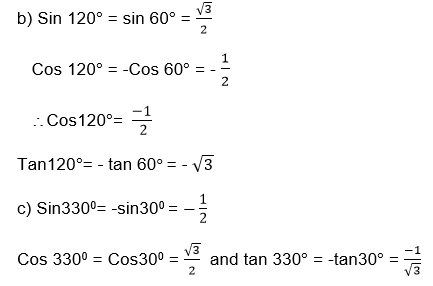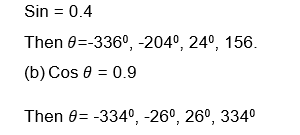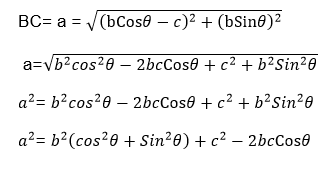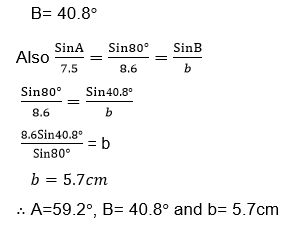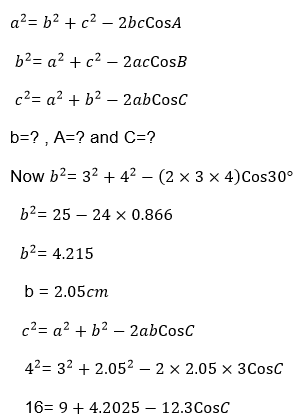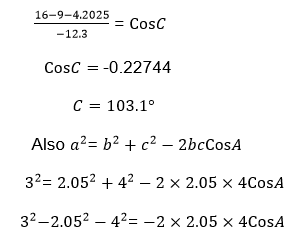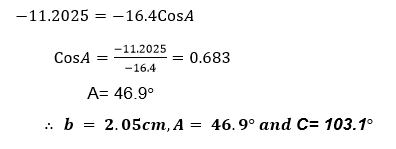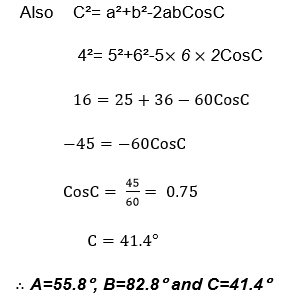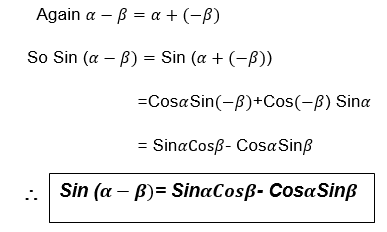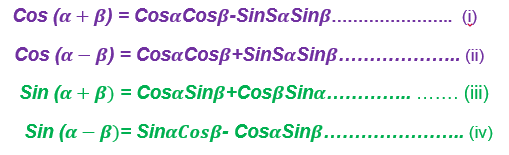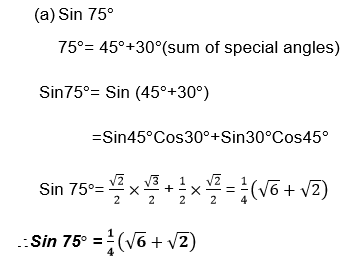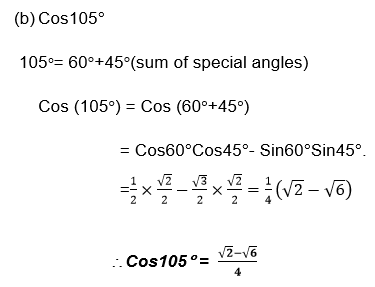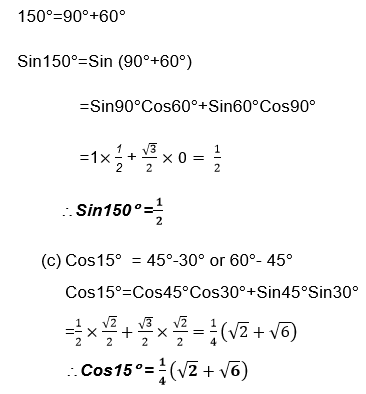FORM FOUR MATHEMATICS TOPIC 5:TRIGONOMETRY

September 14, 2021 , ,

    •  TRIGONOMETRY

    Trigonometry is a branch of mathematics that deals with relationship (s) between angles and sides of triangles.
    The Sine, Cosine and Tangent of an Angle Measured in the Clockwise and Anticlockwise Directions
    Determine the sine, cosine and tangent of an angle measured in the clockwise and anticlockwise directions
    The basic three trigonometrical ratios are sine, cosine and tangent which are written in short as Sin, Cos, and tan respectively.
    Consider the following right angled triangle.
    Also we can define the above triangle ratios by using a unit Circle centered at the origin.
    If θis an obtuse angle (900<θ<180 style="box-sizing: border-box;" sup="">0
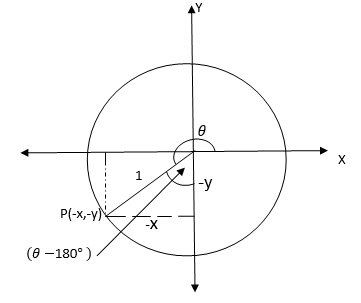
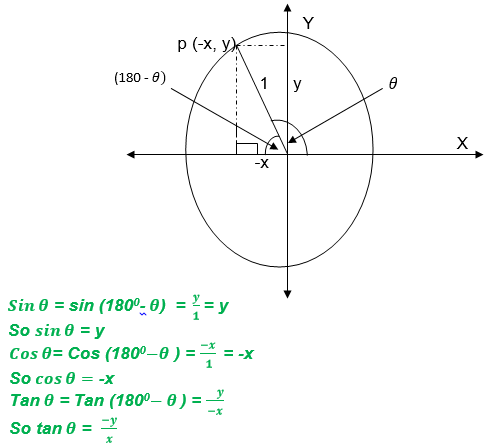
    ) then the trigonometrical ratios are the same as the trigonometrical ratio of 1800-θ
    If θis a reflex angle (1800< θ<270 style="box-sizing: border-box;" sup="">0
    ) then the trigonometrical ratios are the same as that of θ- 1800
    If θis a reflex angle (2700< θ< 3600), then the trigonometrical ratios are the same as that of 3600 -θ
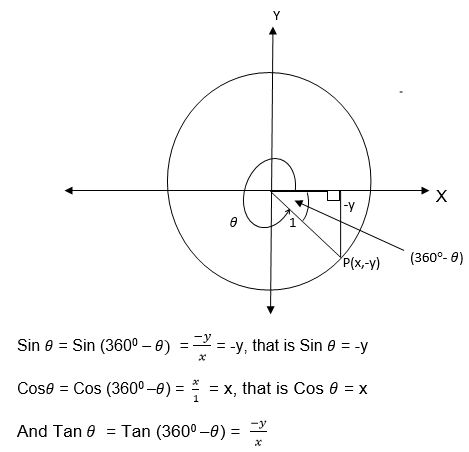
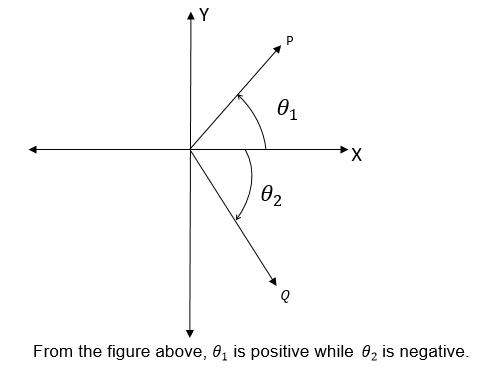
    We have seen that trigonometrical ratios are positive or negative depending on the size of the angle and the quadrant in which it is found.
    The result can be summarized by using the following diagram.
    Trigonometric Ratios to Solve Problems in Daily Life
    Apply trigonometric ratios to solve problems in daily life
    Example 1
    Write the signs of the following ratios
    1. Sin 1700
    2. Cos 2400
    3. Tan 3100
    4. sin 300
    Solution
    a)Sin 1700
    Since 1700 is in the second quadrant, then Sin 1700 = Sin (1800-1700) = Sin 100
    ∴Sin 1700 = Sin 100
    b) Cos 2400 = -Cos (2400-1800)= -Cos 600
    Therefore Cos 2400= -Cos 600
    c) Tan 3100 = -Tan (3600-3100) = - Tan 500
    Therefore Tan 3100= -Tan 500
    d) Sin 3000= -sin (3600-3000) = -sin 600
    Therefore sin 3000= - Sin 600
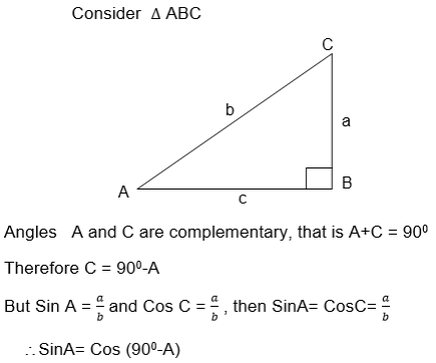
    Relationship between Trigonometrical ratios
    The above relationship shows that the Sine of angle is equal to the cosine of its complement.
    Also from the triangle ABC above
    Again using the ΔABC
    b2 = a2+c2 (Pythagoras theorem)
    And
    Example 2
    Given thatA is an acute angle and Cos A= 0.8, find
    1. Sin A
    2. tan A.
    Example 3
    If A and B are complementary angles,
    Solution
    If A and B are complementary angle
    Then Sin A = Cos B and Sin B = Cos A
    Example 4
    Given that θand βare acute angles such that θ+ β= 900 and Sinθ= 0.6, find tanβ
    Solution
    Exercise 1
    For practice



















    Sines and Cosines of Angles 0 Such That -720°≤ᶿ≥ 720°
    Find sines and cosines of angles 0 such that -720°≤ᶿ≥ 720°
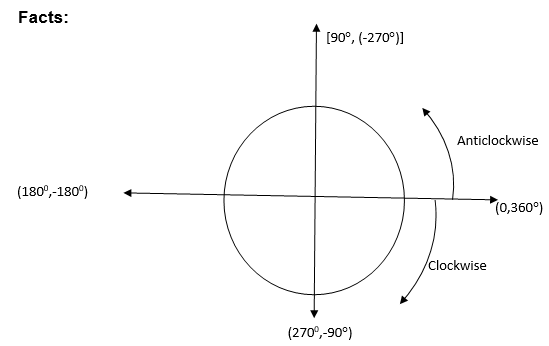
    Positive and Negative angles
    An angle can be either positive or negative.
    Definition:
    Positive angle: is an angle measures in anticlockwise direction from the positive X- axis
    Negative angle: is an angle measured in clockwise direction from the positive X-axis
    Facts:
    1. From the above figure if is a positive angle then the corresponding negative angle to is (- 3600) or (+ - 3600)
    2. .If is a negative angle, its corresponding positive angle is (360+)
    Example 5
    Find thecorresponding negative angle to the angle θif ;
    1. θ= 580
    2. θ= 2450
    Example 6
    What is the positive angle corresponding to - 46°?
    SPECIAL ANGLES
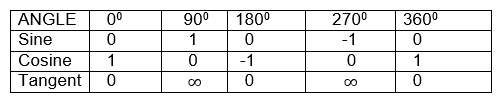
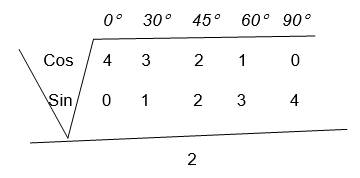
    The angles included in this group are 00, 300, 450, 600, 900, 1800, 2700, and 3600
    Because the angle 00, 900, 1800, 2700, and 3600, lie on the axes then theirtrigonometrical ratios are summarized in the following table.
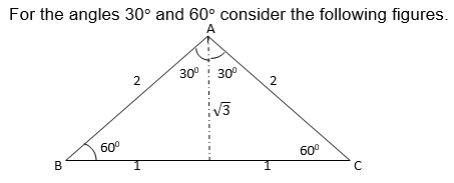
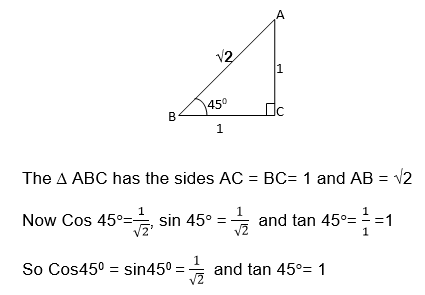
    The ∆ ABC is an equilateral triangle of side 2 units
    For the angle 450 consider the following triangle
    The following table summarizes the Cosine, Sine, and tangent of the angle 300 , 450 and 600
    NB: The following figure is helpful to remember the trigonometrical ratios of special angles from 0°to 90°
    If we need the sines of the above given angles for examples, we only need to take the square root of the number below the given angle and then the result is divided by 2.
    Example 7
    Find the sine,cosine and tangents of each of the following angles
    1. -1350
    2. 1200
    3. 3300
    Example 8
    Find the value of θif Cos θ= -½ and θ≤ θ≤ 360°
    Solution
    Since Cos θis – (ve), then θlies in either the second or third quadrants,
    Now - Cos (180 –θ= - Cos (θ+1800) = -½= -Cos600
    So θ= 1800-600 = 1200 or θ= 1800 + 600 = 2400
    θ= 1200 0r θ=2400
    Example 9
    Consider below
    Exercise 2
    Solve the Following.
    The Graphs of Sine and Cosine
    Draw the graphs of sine and cosine
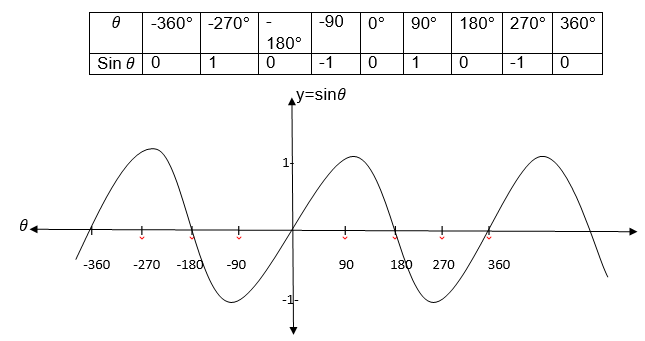
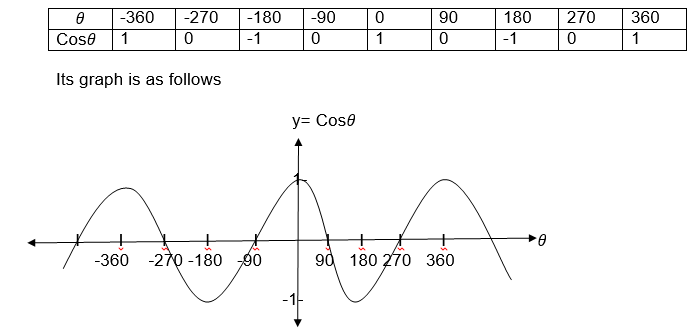
    Consider the following table of value for y=sinθ where θranges from - 360°to 360°
    For cosine consider the following table of values
    From the graphs for the two functions a reader can notice that sinθand cosθboth lie in the interval -1 and 1 inclusively, that is -1≤sinθ1 and -1≤cosθ≤1 for all values of θ.
    The graph of y= tanθis left for the reader as an exercise
    NB: -∞≤ tanθ≤∞the symbol ∞means infinite
    Also you can observe that both Sinθnd cosθrepeat themselves at the interval of
    360°, which means sinθ= sin(θ+360) = sin(θ+2x3600) etc
    and Cosθ=(Cosθ+3600)= Cos(θ+2x3600)
    Each of these functions is called a period function with a period 3600
    1. Usingtrigonometrical graphs in the interval -3600≤θ≤3600
    Find θsuch that
    1. Sin= 0.4
    2. Cos= 0.9
    solution
    Example 10
    Use the graph of sinθto find the value ofθif
    4Sinθ= -1.8 and -3600 ≤θ≤3600
    Solution
    4Sinθ= -1.8
    Sinθ= -1.8÷4 = -0.45
    Sinθ= -0.45
    So θ= -1530, -270, 2070, 3330
    The graphs of sine and cosine functions
    Interpret the graphs of sine and cosine functions
    Example 11
    Use thetrigonometrical function graphs for sine and cosine to find the value of
    1. Sin (-400)
    2. Cos (-400)
    Solution
    1. Sin (-400)= - 0.64
    2. Cos (-400)= 0.76

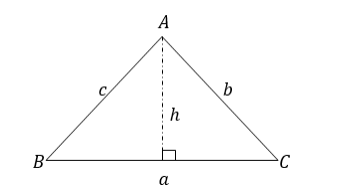
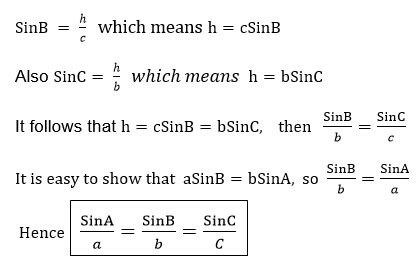
    The Sine and Cosine Rules
    Derive the sine and cosine rules
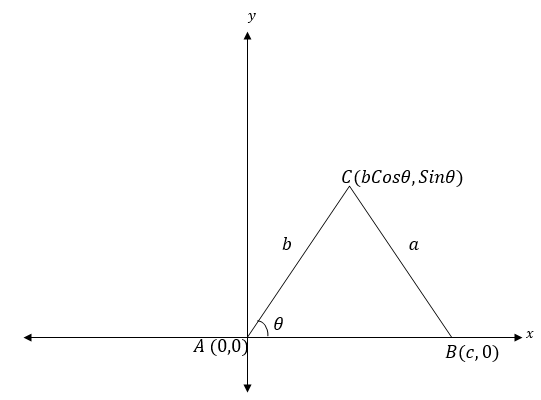
    Consider the triangle ABC drawn on a coordinate plane
    From the figure above the coordinates of A, B and C are (0, 0), (c, 0) and(bCosθ, bSinθ) respectively.
    Now by using the distance formula
    SINE RULE
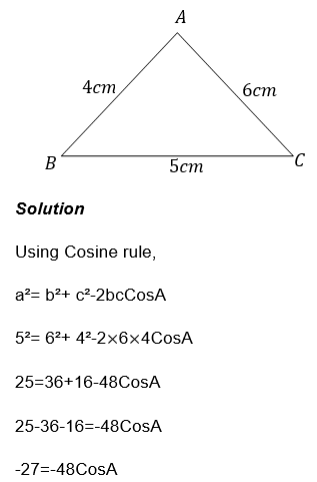
    Consider the triangle ABC below
    From the figure above,
    Note that this rule can be started as “In any triangle the side are proportional to the Sines of the opposite angles”
    The Sine and Cosine Rules in Solving Problems on Triangles
    Apply the sine and cosine rules in solving problems on triangles
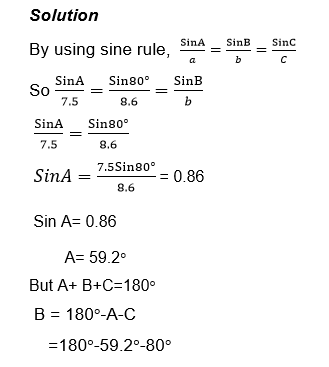
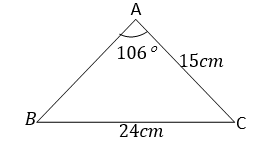
    Example 12
    Find the unknown side and angle in a triangle ABC given that
    a= 7.5cm
    c= 8.6cm and C= 80°
    Find the unknown sides and angle in a triangle ABC in which a= 22.2cmB= 86°and A= 26°
    Solution
    By sine rule
    Sin A= sin B= Sin C
    Example 13
    Find unknown sides and angles in triangle ABC
    Where a=3cm, c= 4cm and B= 30°
    Solution
    By cosine rule,
    Example 14
    Find the unknown angles in the following triangle
    Exercise 3
    1. Given thata=11cm, b=14cm and c=21cm, Find the Largest angle of ΔABC
    2. If ABCD is a parallelogram whose sides are 12cm and 16cm what is the length of the diagonal AC if angle B=119°?
    3. A and B are two ports on a straight Coast line such that B is 53km east of A. A ship starting from A sails 40km to a point C in a direction E65°N. Find:
    1. The distance a of the ship from B
    2. The distance of the ship from the coast line.
    4. Find the unknown angles and sides in the following triangle.
    5. A rhombus has sides of length 16cm and one of its diagonals is 19cm long. Find the angles of the rhombus.
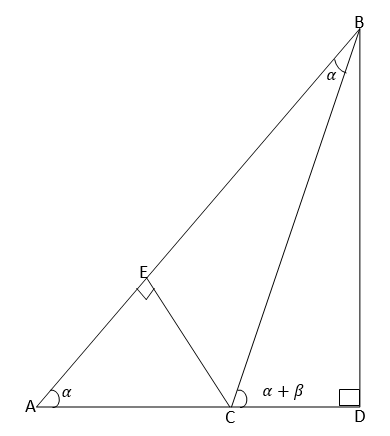
    The Compound of Angle Formulae or Sine, Cosine and Tangent in Solving Trigonometric Problems
    Apply the compound of angle formulae or sine, cosine and tangent in solving trigonometric problems
    The aim is to express Sin (α±Î²) and Cos (α±Î²) in terms of Sinα, Sinβ, Cosαand Cosβ
    Consider the following diagram:
    From the figure above
    From ΔBCD
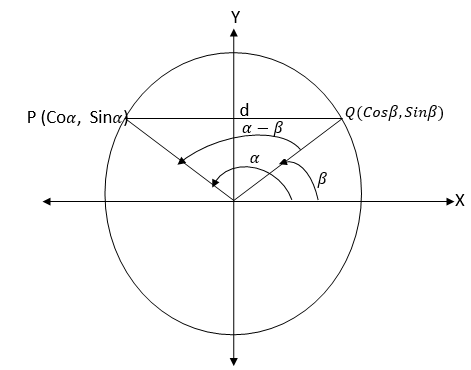
    For Cos(α±Î²) Consider the following unit circle with points P and Q on it such that OP,makes angleα with positive x-axis and OQ makes angle βwith positive x-axes.
    From the figure above the distance d is given by
    In general
    Example 15
    1. Without using tables find the value of each of the following:
    1. Sin 75°
    2. Cos 105
    Solution:
    Example 16
    Find:
    1. Sin150°
    2. Cos 15°
    Exercise 4
    1. Withoutusing tables, find:
    1. Sin 15°
    2. Cos 120°
    2. Find Sin 225° from (180°+45°)
    3. Verify that
    1. Sin 90° = 1 by using the fact that 90°=45°+45°
    2. Cos90°=0 by using the fact that 90°=30°+60°
    4. Express each of the following in terms of sine, cosine and tangent of acute angles.
    1. Sin107°
    2. Cos300°
    5. By using the formula for Sin (A-B), show that Sin (90°-C)=Cos C
















    Post a Comment

    No comments

    Subscribe to: Post Comments ( Atom )